Henrique K. Miyamoto

Doctoral researcher

Research

Production

Journal papers

[J4] H. K. Miyamoto, F. C. C. Meneghetti, J. Pinele and S. I. R. Costa, “On closed-form expressions for the Fisher-Rao distance”, Information Geometry, vol. 8, pp. 311-354, 2024, doi: 10.1007/s41884-024-00143-2. [Link] [arXiv]

[J3] H. K. Miyamoto, F. C. C. Meneghetti and S. I. R. Costa, “The Fisher-Rao loss for learning under label noise”, Information Geometry, vol. 6, pp. 107-126, 2023, doi: 10.1007/s41884-022-00076-8. [Link] [arXiv]

[J2] H. K. Miyamoto and S. Yang, “Context-tree-based lossy compression and its application to CSI representation”, IEEE Transactions on Communications, vol. 70, no. 7, pp. 4417-4428, 2022, doi: 10.1109/TCOMM.2022.3173002. [Link] [arXiv]

[J1] H. K. Miyamoto, S. I. R. Costa and H. N. Sá Earp, “Constructive spherical codes by Hopf foliations”, IEEE Transactions on Information Theory, vol. 67, no. 12, pp. 7925-7939, 2021, doi: 10.1109/TIT.2021.3114094. [Link] [arXiv]

Conference papers

[C8] H. K. Miyamoto and S. Yang, “On universal decoding over memoryless channels with the Krichevsky–Trofimov estimator”, IEEE International Symposium on Information Theory (ISIT), Athens, 2024, pp. 1498-1503, doi: 10.1109/ISIT57864.2024.10619414. [Link]

[C7] H. K. Miyamoto, “Geometria, Estatística e Aplicações a Comunicações e Aprendizado”, Proceeding Series of the Brazilian Society of Computationa and Applied Mathematics, vol. 10, no. 1, 2023 (in Portuguese), doi: 10.5540/03.2023.010.01.0004. [Link]

This is an extended abstract of [T1], published for the Clóvis Caesar Gonzaga Award (SBMAC 2023).

[C6] F. C. C. Meneghetti, H. K. Miyamoto, S. I. R. Costa and M. H. M. Costa, “Revisiting lattice tiling decomposition and dithered quantisation”, Geometric Science of Information (GSI), Saint-Malo, 2023. In: F. Nielsen and F. Barbaresco (eds.), GSI 2023, LNCS 14071, pp. 318-327, Springer, 2023, doi: 10.1007/978-3-031-38271-0_319. [Link]

[C5] F. C. C. Meneghetti, H. K. Miyamoto and S. I. R. Costa, “Information properties of a random variable decomposition through lattices”, 41st International Conference on Bayesian and Maximum Entropy Methods in Science and Engineering (MaxEnt 2022), Paris (hybrid), 2022. In: Physical Sciences Forum, vol. 5, no. 1, 2022, doi: 10.3390/psf2022005019. [Link]

[C4] H. K. Miyamoto and S. Yang, “A CSI compression scheme using context trees”, International Zurich Seminar on Information and Communication (IZS), Zurich, 2022, pp. 24-28, doi: 10.3929/ethz-b-000535273. [Link]

[C3] H. K. Miyamoto, H. N. Sá Earp and S. I. R. Costa, “Constructive spherical codes in \(2^k\) dimensions”, IEEE International Symposium on Information Theory (ISIT), Paris, 2019, pp. 1612-1616, doi: 10.1109/ISIT.2019.8849464. [Link]

[C2] H. K. Miyamoto, H. N. Sá Earp and S. I. R. Costa, “Construção de códigos esféricos usando a fibração de Hopf”, Jornada Nacional de Iniciação Científica (JNIC), 70ª Reunião Anual da SBPC, Maceió, 2018 (in Portuguese), ISSN: 2176-1221. [Link]

[C1] H. K. Miyamoto, H. N. Sá Earp and S. I. R. Costa, “Construction of spherical codes using the Hopf fibration”, XXV Congresso de Iniciação Científica da Unicamp, Campinas, 2017, doi: 10.19146/pibic-2017-78809. [Link]

Presentations

[A9] “On universal decoding over memoryless channels with the Krichevsky–Trofimov estimator” (poster presentation), IEEE European School on Information Theory (ESIT), Eindhoven, Netherlands, 2024.

[A8] “On universal decoding over memoryless channels with the Krichevsky–Trofimov estimator” (poster presentation), France PhD Workshop on Information Theory, Palaiseau, France, 2024.

[A7] “Universal decodig with context trees” (poster presentation), IEEE European School on Information Theory (ESIT), Bristol, UK, 2023.

[A6] “Universal decodig with context trees” (poster presentation), Journée des Doctorants en STIC du Plateau de Saclay, Palaiseau, France, 2023.

[A5] “The Fisher-Rao loss for learning under label noise” (oral presentation), International Conference on Information Geometry for Data Science (IG4DS), Hamburg, Germany (virtual), 2022.

[A4] “Construction of spherical codes using the Hopf fibration” (short communication), International Congress of Mathematicians (ICM), Rio de Janeiro, Brazil, 2018. [Link]

[A3] “A recursive algorithmic construction for spherical codes in dimensions \(\mathbb{R}^{2^k}\)” (poster presentation), Latin American Week on Coding and Information (LAWCI), Campinas, Brazil, 2018.

[A2] “Construção de códigos esféricos usando a fibração de Hopf” (oral presentation), Seminários DivulgaMat, IMECC/Unicamp, Campinas, Brazil, 2018. [Link]

[A1] “Construção de códigos esféricos usando a fibração de Hopf” (oral presentation), Jornada de Matemática, Matemática Aplicada e Educação Matemática (J3M), Curitiba, Brazil, 2017. [Link]

Patent applications

[P1] I. Land, H. K. Miyamoto, A. Destounis and J. C. Belfiore, “Transfer Learning between Neural Networks”, patent applications WO202207097, CN117121020, EP2021716362, 2021. [WIPO] [EPO] [Google Patents]

Theses

[T1] H. K. Miyamoto, “Geometria, Estatística e Aplicações a Comunicações e Aprendizado”, Master’s dissertation in applied mathematics, Universidade Estadual de Campinas, 2022 (in Portuguese). [Link] [PDF] [Errata]

Received the Clóvis Caesar Gonzaga Award for best master’s dissertation in applied and computational mathematics (SBMAC 2023).

Projects

From universal compression to universal communications

Universal compression schemes are those that, despite not being aware of the distribution of the source (only its class), can attain the same asymptotic performance as if they were; namely their average codeword length converges to the entropy rate. A problem that is in some sense dual to this one is universal decoding: this refers to decoding schemes that, being ignorant of the channel statistics (only its class), obtain the same asymptotic random-coding error exponent as a maximum-likelihood decoder. In this project we aim to explore fundamental results and practical applications of universal decoding, using the relation between universal compression and universal decoding.

This is a Ph.D. project under supervision of Prof. Sheng Yang at the Laboratory of Signals and Systems (L2S), Université Paris-Saclay.

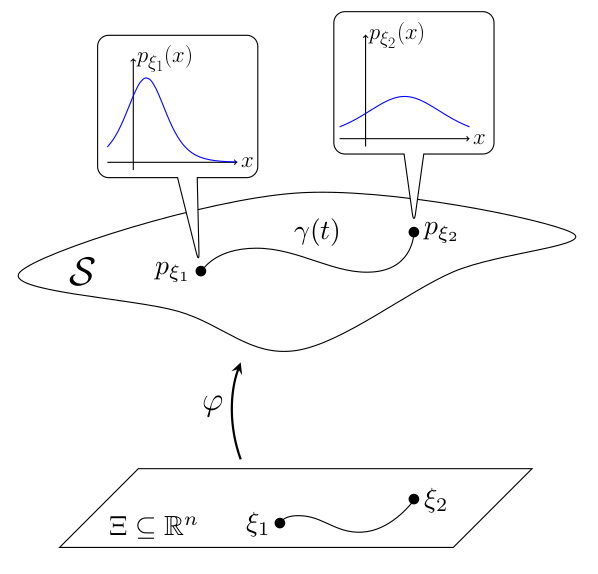
Information geometry and applications

Information geometry studies the intrinsic geometry of probability distribution families by regarding them as statistical manifolds. It is knwon that the metric given by the Fisher information matrix is essentially the unique Riemannian metric invariant under sufficient statistics on such manifolds; this metric induces a natural notion of distance between probability distributions from the same family, the so-called Fisher-Rao distance. In this project, we aim to apply information-geometric methods to problems in machine learning.

This project started as a master's project from 2021 to 2022, under supervision of Prof. Sueli I. R. Costa, at the Institute of Mathematics, Statistics and Scientific Computing (IMECC), Unicamp. It was supported by FAPESP grant no. 21/04516-8.

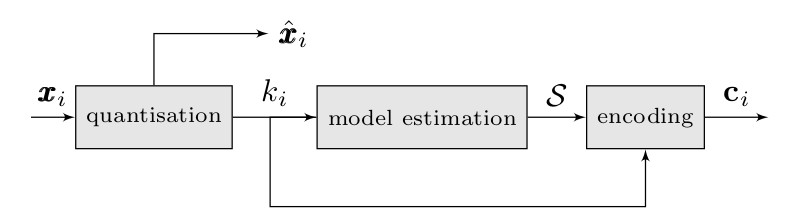
Data compression for wireless communications

For different purposes in communications, such as feedback and storage, it is necessary to represent the channel state information (CSI) in an ‘economical’ way. When the statistics of underlying process is unknown, an universal compression algorithm, such as Lempel-Ziv and CTW can be used. We propose a context-tree-based approach for compressing time-varying CSI, which combines lossy vector quantisation, by means of data-adapted companders, with lossless compression, based on symbol probabilities estimated by a context-tree model.

This project started as a summer internship developped under supervision of Prof. Sheng Yang, at the Laboratory of Signals and Systems (L2S), CentraleSupélec.

See more about this work here.

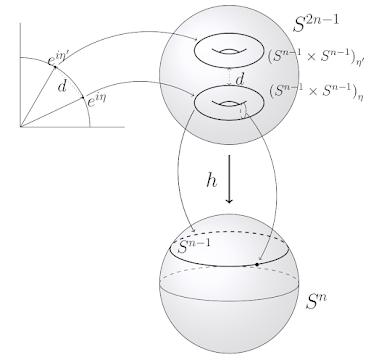
Spherical codes by Hopf foliations

Spherical codes are discrete sets of points on the surface of an Euclidean sphere, and have several applications in sicences and engineering. Problems with spherical codes involve finding optimal distributions of points relative to some parameter of interest, such as the minimum distance between two points. We address the spherical packing problem in dimensions \(2^k\), and propose a construction for spherical codes in such dimensions by exploiting the structure of sphere foliations induced by the Hopf fibration. This procedure outperforms some current constructive methods in several small-distance regimes and constitutes a compromise between coding rate and effective constructiveness with low encoding complexity.

This project started as an undergraduate research ("iniciação científica") project developped at the Institute of Mathematics, Statistics and Scientific Computing (IMECC), Unicamp, from 2016 to 2018, under supervision of Prof. Henrique N. Sá Earp and Prof. Sueli I. R. Costa. It was supported by FAPESP grant no. 16/05126-0, as part of the thematic project Security and reliability of information: theory and practice (13/25977-7), of which Prof. Costa was a main researcher.

Collaborators

This is a list of people with whom I have collaborated:

“Mathematical discovery is by no means a matter of systematic deductive procedure. It involves insight, imagination, and long explorations along paths that sometime lead nowhere.”

— Robert Goldblatt in Topoi: The Categorial Analysis of Logic, p. 14